Funky is a new, small programming language that's like and unlike any other language you've seen before.

It's purely functional, doesn't cheat, but unlike most languages in this space, Funky lets you structure your code top to bottom. Idiomatic Funky code often reads like a well-written imperative algorithm. This lends code that is natural to read - yet in the end, it's basically just λ-calculus.

Funky aims for simplicity and joy. No categories, no monads, no weird abstract math operators. Nothing unnecessary. Funky is a pragmatic language for programmers.

A small warning. Funky was created from scratch. While the standard, battle-tested, functional core, like map, filter, Maybe, etc. will be familiar to all functional programmers, many things will surprise you. For example, as we'll soon discover, let and if are not built-in to the language. Instead, they're functions just like any other. Many more surprises await you in the tour.

So, here we go!

Credit! All the beautiful art in this tour (including the picture above) have been crafted by the talented girl Tori Bane. You can check out her Instagram or buy her a Ko-fi.

Note. These instructions are for Linux. If you're on another operating system, you can try to follow them doing analogous actions on your OS.

Funky is currently implemented in Go and there are no pre-compiled binaries provided yet.

Therefore, the first step is to install the Go language either from the official website or from your package manager.

Go uses $GOPATH directory to download packages and install Go programs. If you installed a recent version of Go, you don't have to set it up, it defaults to ~/go.

Next, you need to download Funky. You do that with the Go package manager:

$ go get -u github.com/faiface/funky/...

This downloads Funky repository to the $GOPATH/src directory and installs the binaries to the $GOPATH/bin directory.

To make the binaries easily runnable from the command line, you need to add $GOPATH/bin (or ~/go/bin if $GOPATH is not set) to the $PATH environment variable. Add this to your ~/.bashrc file (or an equivalent of that for your shell):

# replace $GOPATH with /home/yourname/go if $GOPATH is not set up
export PATH=$PATH:$GOPATH/bin

Now, one last thing. Funky uses the $FUNKY environment variable to identify the location of the standard library. Add this to your .bashrc file:

export FUNKY=$GOPATH/src/github.com/faiface/funky/stdlib

And that's it! Let's get ready for some action!

Let's make sure everything works. Open your favorite text editor and put in these lines:

func main : IO =
    println "Hello, world!";
    quit

Now hit the command line and type this:

$ funkycmd hello.fn
Hello, world!

There we go!

It should work. If it doesn't, go back and see if you set everything up correctly. If you did and it still doesn't work, file an issue.

Funky is a strongly typed language. To explore types, Funky provides a types sandbox. It's kind of like a REPL, but it doesn't evaluate anything - just tells you the types.

Here's how we fire it up:

$ funkycmd -types
>

Note. funkycmd -types currently doesn't implement convenient things like 'arrow up' to go back to the previous entry, and so on. To get those, I highly recommend using the rlwrap utility. Just install it and run rlwrap funkycmd -types and you'll get all those convenient features.

It opens up a little prompt where we can type expressions. Let's try it!

$ funkycmd -types
> 5
Int
> 3.14
Float
> pi
Float
> 'x'
Char

Details. Funky has three built-in types: Int, Float, and Char. Ints are arbitrary-precision integers. Floats are IEEE-754 64-bit floating-point numbers. Chars are Unicode characters. All other types are either from the standard library or defined by the programmer.

How about using some operators and functions?

> 13 + 48
Int
> sqrt 4
sandbox:1:6: type-checking error

Ugh, what? A type-checking error? Yeah, that's right.

Note. The compiler error messages will get better and more descriptive.

> sqrt
Float -> Float
> 4
Int

As we can see, the type of the sqrt function is Float -> Float (a function that takes a Float and returns a Float), while the value we supplied is an Int. This doesn't match. Instead, we need to supply a Float value:

> sqrt 4.0
Float

Now this works.

Details. There are many built-in functions for each of these built-in types. Arithmetic operators (+, -, *, /, ^, %), comparison operators (==, !=, <, >, <=, >=), math functions (sin, cos, sqrt, atan2, etc.), and conversion functions (float, int, etc.). One notable thing is that you can't add characters - 'a' + 'b' is not valid - but you can add an integer to a character: 'a' + 2 results in 'c'.

Note. Unary minus is not spelled -, but neg. The reason is that - is always infix because of its name. You can still use - in number literals, like -42.

We've already printed "Hello, world!", how about printing other stuff? Let's try:

func main : IO =
    println 13;
    quit

Try running it:

$ funkycmd hello.fn
hello.fn:2:13: type-checking error

A type-checking error again? Let's see where we went wrong. Start up the types sandbox:

$ funkycmd -types
>

And let's examine the type of the println function:

> println
String -> IO -> IO

Oh, so the println function only takes strings. Could've guessed that!

Note. Although it might not seem like it at first, println is a completely pure function. It takes two arguments: a String and an IO. The IO is a continuation - it says what should be done after the string gets printed. In our case, the continuation is quit (which has the type IO itself). This instructs the program to quit after printing the string. The precise workings of this will be explained soon.

So, how do we convert an Int or a Float to a String so that we can print it?

The string function is for that purpose. Let's see what's the type of this string function:

$ funkycmd -types
> string
Int -> String
Float -> String
Bool -> String
Char -> String
String -> String

Details. Bool and String are not built-in, they're implemented in the standard library.

Wait, what? The string function has multiple types? That's exactly correct!

Unlike most functional languages, Funky supports overloading. That means that you can define many functions with the same name, provided they are distinguishible by their types.

Back to the printing. This now works:

func main : IO =
    println (string 13);
    quit

Runs as expected:

$ funkycmd hello.fn
13

Exercise. Play with various functions. Try operators like *, ^, %, math functions like sqrt, sin, log, booleans true and false, string functions ++, *, and so on. The types sandbox tells you what exists and what types it has.

You've probably noticed the semicolon we used in the previous part and wondered what that's for. Its meaning is actually very simple. It's used to separate the last argument to a function without the need to put it in parentheses. Let's see. Say we have an expression like this:

string (sqrt 4.0 + sqrt 9.0)

We can omit the parentheses and use the semicolon instead:

string; sqrt 4.0 + sqrt 9.0

Note. If you're familiar with Haskell, you'll notice that the semicolon is just like Haskell's $ operator. That's correct. Funky uses the semicolon instead of the dollar to avoid visual clutter because it's used very frequently.

The semicolon becomes very useful when structuring code. We could write this:

func main : IO =
    println "A" (println "B" (println "C" quit))

That's a completely valid code that prints three lines:

$ funkycmd abc.fn
A
B
C

Explanation. If you're having trouble understand the code above, here's an explanation. The IO is a data structure that describes what the program should do. The simplest IO value is quit. It simply instructs the program to quit.

The type of the println function is String -> IO -> IO. That means that println takes two arguments, a String and an IO, and evaluates to an IO. The resulting IO describes a program that first prints the provided string, then does whatever the second argument says.

Let's look at the innermost (last) usage of println in the above code: println "C" quit. This expression of type IO describes a program that prints the string "C" and then quits. Since it is an IO, we can pass it as the second argument to another println and we get println "B" (println "C" quit). And using the same technique once again, we end up with the code above.

But, we have a lot of parentheses there! Let's get rid of them with those semicolons:

func main : IO =
    println "A"; println "B"; println "C"; quit

Note. We technically don't need the last semicolon as quit is just a single word, but we'll leave it there for style.

And finally, we can split it into multiple lines:

func main : IO =
    println "A";
    println "B";
    println "C";
    quit

Now that's cool! It's got lines, it's got semicolons, looks just like an imperative code! Of course, I'm joking a bit here, but it's not that bad, is it?

Booleans have type Bool, two values - true and false - and a handy if function for making a choice. What's its type? The beloved types sandbox comes to the rescue:

$ funkycmd -types
> if
Bool -> a -> a -> a

The little a is a type variable. You can replace it with any type whatsoever and if will conform to that type. Of course, you must replace all occurences of a consistently. So if can be used as Bool -> Int -> Int -> Int, or as Bool -> IO -> IO -> IO, but not as Bool -> Int -> IO -> Float.

The if function checks whether the condition (the first argument) is true or false. If it's true, the second argument is returned. Otherwise, the third argument is returned. For example:

> if true 1 3            # evaluates to 1
Int
> if (4 < 1) "YES" "NO"  # evaluates to "NO"
List Char

Note. Comments start with the # symbol. Also, notice that String and List Char are synonyms.

Combining the if function with the semicolon, we create an if, else if, else chain:

if (guess > correct) "Less.";
if (guess < correct) "More.";
"Correct!"

Isn't that beautiful? A single function suitable both for a one-line choice and for a series of mutually exclusive branches.

Funky has a very concise syntax for anonymous functions. That's crucial because just like semicolons, anonymous functions are used all over the place. Here's how you write them:

\variable result

That's it. A backslash, a name for the variable, and an expression to evaluate to.

Important. All identifiers in Funky are allowed to contain almost arbitrary Unicode characters. That's because tokens are generally separated by whitespace. The only exceptions are the symbols (, ), [, ], {, }, ,, ;, \, and # that are always parsed as separate tokens.

Therefore, idiomatic naming in Funky is very similar to the one in LISP. Dashes are-used instead of_underscores, functions returning Bool (predicates) usually end with the ? symbol and partial functions (those that can crash) end with the ! symbol.

Functions of multiple arguments are just functions that take the first argument and return a function taking the rest of the arguments (currying):

\x \y x + y

Funky uses lazy evaluation. That means that arguments to functions are only evaluated when their value is needed. For example, the factorial of 20 is never calculated here:

(\n 3) (factorial 20)  # evaluates to 3

Also, the factorial of 10 is only computed once, not twice here:

(\n n + n) (factorial 10)

The let function? Not a let keyword? Let's verify this:

$ funkycmd -types
> let
a -> (a -> c) -> c

Note. It really should be a -> (a -> b) -> b. Will be fixed.

Uhm, so let takes a value and a function. Yep, and then it passes the value to the function and evaluates to whatever the function evaluates to. Maybe a bit hard to understand, so let's see:

func main : IO =
    println (string; let 7 (\x x + x));
    quit

See that let 7 (\x x + x) there? From what I've said, let should pass the 7 to the (\x x + x) function and thus the program should print 14. And in fact that's exactly what happens:

$ funkycmd let.fn
14

But as you've probably guessed, this is not the idiomatic use of let. Let's take a closer look:

let 7 (\x x + x)

That's pretty ugly! There's one syntactic feature, though, that we haven't talked about yet. If a lambda is the last argument to a function, which it is in our case, we can drop the parentheses. Like this:

let 7 \x x + x

And what now? Split it into multiple lines!

let 7 \x
x + x

Now it's starting to look like something. It looks like we've assigned the value 7 to the variable x and then went on to the next code. And that's precisely how we should think about it. In fact, we can restructure our little program above like this:

func main : IO =
    let 7 \x
    println (string; x + x);
    quit

In this case, the type of the let function got specialized to Int -> (Int -> IO) -> IO, but the result is the same.

So, that's how you assign variables in Funky.

Funky has an unusual approach to side-effects. There's no notion of them in the language itself. What looked like side-effecting functions in the previous sections (println, quit, etc.) were, in fact, data structure constructors. The IO type is not magic at all. It's just a plain data structure defined in the Funky language itself. Here's its definition (you can also find it in the standard library in the cmd folder):

union IO = quit | putc Char IO | getc (Char -> IO)

We haven't covered union yet but think algebraic data types (e.g. data in Haskell). This IO data structure serves as a description of what the program should do. However, in contrast with the control flow of traditional imperative languages, the IO data structure can be arbitrarily manipulated - e.g. it's no problem to implement input/output encryption just by implementing a single IO -> IO function.

Note. The IO data structure is very limited. All it can express is printing and scanning characters. The thing we haven't talked about yet is that funkycmd is just one of the many possible side-effect interpreters. Specifically, funkycmd interprets (executes) the above IO data structure. There's another interpreter called funkygame that interprets an entirely different data structure which describes sprite-based games. You can actually make your own side-effect interpreter fairly easily. The specifics of that are explained in another part.

The IO looks like a linked list with two kinds of nodes (not counting quit). The funkycmd interpreter loads the main function, walks the IO nodes, and does as they say.

Let's talk about the nodes individually.

• quit. We've seen this one before - it marks the end of the program.

• putc. This node has two arguments: a Char and an IO. The Char is the character to be printed. The IO tells what should be done next.

• getc. Now this one looks strange. It has one argument: a function. The function takes a Char and returns an IO. Here's how funkycmd deals with getc: Upon encountering the getc node, funkycmd scans a character from the standard input. Then it takes the function under getc and applies it to the scanned character, passes it inside. The function gives back an IO. This IO tells what should be done next.

Now let's see them in action!

How about a very exciting program that reads a character and prints it back?

func main : IO =
    getc (\c putc c quit)

Run it:

$ funkycmd getcputc.fn
x
x

It worked!

Now, we can structure the code better using the same tricks we used with if and let. How does this look?

func main : IO =
    getc \c
    putc c;
    quit

Well, that's nice! The first line scans a character, the second line prints it back, the third line quits the program.

Wait, what would happen if we made it recursive? What if we replaced quit with main?

func main : IO =
    getc \c
    putc c;
    main

By the looks of it, this program should print back all of its input - it's the cat program.

Note. But it never quits! Or does it? Currently, funkycmd is made to silently quit when encountering the EOF, so the program quits correctly. Of course, this behavior is not guaranteed to be kept.

$ funkycmd cat.fn
hello, cat!
hello, cat!
do you cat?
do you cat?
you do cat!
you do cat!
^D

The ^D sequence at the end is the EOF.

The standard library gives us many goods. There's print and println that work by expanding to multiple putc nodes. Are there some analogous high-level functions for scanning? Sure there are! They're called, how unexpected, scan and scanln. What are their types:

$ funkycmd -types
> scan
(String -> IO) -> IO
> scanln
(String -> IO) -> IO

Oh nice, so their type is the same as the type of getc, except the Char is changed to String.

The scanln function scans a whole line and gives it back to you (not including the newline character). The scan function is a little more clever: it reads the next "word" from the input - it skips all the whitespace and captures a continuous string of non-whitespace characters.

We'll get to use scan more in the next section. Here's some scanln for the taste:

func main : IO =
    print "What's your name? ";
    scanln \name
    println ("Hello, " ++ name ++ "!");
    quit

And there we go:

$ funkycmd greeting.fn
What's your name? Michal Štrba
Hello, Michal Štrba!

We've covered a few basic functions, now we'll put them to the test! We'll make a little calculator. The program is simple but nicely demonstrates how all the functions we've talked about work together. Let's see!

The calculator will work something like this:

$ funkycmd calculator.fn
2 + 2
4
9 / 2
4.5
12 * 12
144

It will support four operators: +, -, *, /. It will only support one operator per expression.

The first thing will be to scan the expression. The expression consists of three words on a single line, so it'll be best to use scan three times:

func main : IO =
    scan \x-str
    scan \op
    scan \y-str
    # TODO

Good. Now, x-str and y-str are strings because that's what scan gives us. In order to perform computations, we need to convert them to floats first.

$ funkycmd -types
> float
Int -> Float
String -> Float

The second overload of the float function seems to be doing just that, so let's use it (there's an analogous function for integers called int):

func main : IO =
    scan \x-str
    scan \op
    scan \y-str
    let (float x-str) \x
    let (float y-str) \y
    # TODO

We saved the converted numbers in the x and y variables.

Now we need to compute the result and print it. For example, if the operator is +, the result will be string; x + y. Here we can exploit the if function's ability to form if/else chains:

if (op == "+") (string; x + y);
if (op == "-") (string; x - y);
if (op == "*") (string; x * y);
if (op == "/") (string; x / y);
"invalid operator: " ++ op

The last line becomes the result if the operator is not among the supported ones. Now that we've got the result, all that's left it to print it and continue the loop:

func main : IO =
    scan \x-str
    scan \op
    scan \y-str
    let (float x-str) \x
    let (float y-str) \y
    println (
        if (op == "+") (string; x + y);
        if (op == "-") (string; x - y);
        if (op == "*") (string; x * y);
        if (op == "/") (string; x / y);
        "invalid operator: " ++ op
    );
    main

And that's it! Now go and experiment yourself! When you come back, we'll start learning about making our own functions and types.

Until now, you've been learning about a few established functions and concepts in the Funky programming language. Now we'll learn how to create our own!

So far, we've only seen one function defined: the main function. But even from that alone, I'm sure you've already guessed how function definitions look. They're quite simple:

func name : type = body

That's it!

The name can be any string of non-whitespace characters excluding keyword symbols like parentheses, a backslash, a semicolon, and a few others.

The type specifies the type that the function name will acquire.

The body is an arbitrary Funky expression, functions, lambda, etc. can be used. The only limitation is that it must conform to the type.

Details. Let's talk a bit about types.

As we've already learned, there are three built-in types: Int, Float, and Char. There are also a few types from the standard library, such as Bool, or String.

Then there are types that take other types as arguments - types that are, so-called, generic. The most important of such generic types is the function type. This is also actually built-in, but since it's a type constructor, rather than a full, distinct type, I haven't included it among the built-in types previously.

The function type constructor is called 'the arrow', written as: ->. It takes two arguments, the input type on the left and the output type on the right. For example, Int -> Bool is a function that takes an Int and evaluates to a Bool.

So, let's define a function! Every functional language tutorial must include a factorial example, so let's get that behind us:

func factorial : Int -> Int =
    \n
    if (n <= 0) 1;
    n * factorial (n - 1)

func main : IO =
    print "Type a number: ";
    scanln \n-str
    let (int n-str) \n
    println (string; factorial n);
    quit

A standard, well known, recursive factorial definition.

Note. In Funky it's a convention to put arguments on the next line after = in the function definition. If the function is very short, this convention may be broken and the whole definition may sit on a single line.

Details. The order of definitions doesn't matter. A function doesn't have to be 'defined before use'. All that matters is that it is defined.

Let's try it:

$ funkycmd factorial.fn
Type a number: 5
120

If it gives 120 for 5 then it surely works. Let's try something bigger:

$ funkycmd factorial.fn
Type a number: 99
933262154439441526816992388562667004907159682643816214685929638952175999932299156089414639761565182862536979208272237582511852109168640000000000000000000000

Whoa, that's a number! You can try entering even bigger inputs, but don't go too big... you may freeze your system.

Now, how about functions with multiple arguments? Say we want to make a function called divides that tells us whether one integer divides another or not.

In Funky, as in many other functional languages, there are no functions of more than one argument. Instead, there are functions that return functions. A function of two arguments really is a function that takes the first argument and returns a new function. This new function remembers the first argument and takes the second one.

What would be the type of such a function?

The type Int -> (Int -> Bool) would do. It takes the first Int, evaluates to a function taking the second Int and finally evaluates to Bool.

Great, now how would we call such a function?

Using (divides 9) 3 would obviously work. But, we don't really need the parentheses. If parentheses are not present, they're implicitly from the left, so divides 9 3 is good too.

Furthermore, the parentheses in the type Int -> (Int -> Bool) aren't needed either. Since -> is used infix, it's automatically parenthesized from the right, so Int -> Int -> Bool is equivalent.

Details. There are two kinds of functions in Funky: prefix and infix. Infix functions can be identified easily: they don't contain any letters. All other functions are prefix.

Applications of prefix functions are automatically parenthesized from the left if no explicit parenthesis are present. In all cases, f x y is the same as (f x) y.

Applications of infix functions are, however, automatically parenthesized from the right. All of them have the same precedence. This is to simplify the programmer's life: when defining own infix functions, you won't be bothered by specifying precedence levels or associativity. So, 3 * 2 + 1 is equivalent to 3 * (2 + 1).

After learning about automatic parentheses (also called left/right-associativity), here's the definition of divides:

func divides : Int -> Int -> Bool =
    \m \n
    (n % m) == 0

The body is just two lambdas nested inside one another, which perfectly reflects the type.

We could've also called the function /?, in which case it would be an infix function. However, the name divides is much more descriptive.

Function types may also contain type variables. These are distinguished from actual types by being all lower-case. Actual types must contain an upper-case character - type variables must not.

When a function has a type variable in its type, that means that this function is fine with whatever type instead of that variable. For example, there's this (probably controversially named function, usually it's called id) function called self:

$ funkycmd -types
> self
a -> a

It doesn't do anything. It just returns whatever it was passed. For example, self 4 is 4. Now, when we passed 4 to self, its type changed a bit. It specialized. It became Int -> Int. See? We get this specialization just by replacing a with Int in the type. That's how type variables work.

Words in natural language usually don't have just one meaning: "If only there was a way we could continue that way, we could've been way ahead of them, but in a way, we haven't done so bad." The previous sentence used four different meanings of the word 'way'.

Using the same words for different, or slightly different meanings in different contexts allows for very concise and expressive speech. Imagine that we'd have to invent a brand new word every time we'd like to add a new meaning to an existing word. That would be cumbersome and unnatural.

Programming is no different. When designing Funky, I realized that support for function overloading brings so many benefits that I couldn't ignore it despite the initial difficulty of implementation.

So, let's try it!

func double : Int -> Int =
    \x x * 2

func double : Float -> Float =
    \x x * 2.0

func main : IO =
    println (string; double 9);
    println (string; double 4.3);
    quit

There we go, two versions of double: one for Ints, one for Floats. Let's run it!

$ funkycmd double.fn
18
8.6

Works like charm!

Now, how about defining two functions like this?

func zero : Int = 0

func zero : Float = 0.0

func main : IO =
    println (string zero);
    quit

This time, both versions of zero fit the context because string works for both Ints and Floats. What does the type checker say?

$ funkycmd zeros.fn
zeros.fn:6:21: ambiguous, multiple admissible types:
  Int
  Float

That's right, the type checker complains. We can fix this error with a type annotation. You can add an explicit type to any expression using the : symbol:

func zero : Int = 0

func zero : Float = 0.0

func main : IO =
    println (string (zero : Int));
    quit

All is fine this time:

$ funkycmd zeros.fn
0

Well, okay, those two zero functions are distinguishable by their type. But what if we put the same type?

func lucky-number : Int = 7
func lucky-number : Int = 3

func main : IO =
    println (string lucky-number);
    quit

Which one gets printed? 7 or 3? Make your guesses, ladies, and gentlemen...

Here's what happens:

$ funkycmd lucky-number.fn
lucky-number.fn:2:27: function lucky-number with colliding type exists: test.fn:1:27

Oh, no! It didn't even let us define the second function, because its type collides with the first one.

Funky doesn't let you overload a function if its type collides with an existing version.

Details. When exactly do two types collide?

Do these two functions collide?

func weirdo : a -> a     = self
func weirdo : Int -> Int = (* 2)

Indeed, they do! You might argue that the second one is more specific than the first one, so if both fit the context, the second one should be selected, but this doesn't fly in Funky, because it brings a whole bag of problems.

Instead, I chose simplicity: two types collide whenever their type variables can be substituted such that they become the same type.

For example: a -> Int collides with Float -> a (substitutes to Float -> Int).

Now onto creating our own types!

I'm sure you're familiar with structs from C or records from Pascal. They simply group multiple values into a single value. Records in Funky are very much the same.

They're defined like this:

record Name = field : type, ...

For example:

record Person =
    name : String,
    age  : Int,

Note. Trailing comma is allowed.

The Person type is now a new, non-reproductive way of creating people (pretty revolutionary if you think about it). How do we create one?

Whenever we define a record, Funky generates a constructor function with the same name. Let's see!

$ funkycmd -types person.fn
> Person
String -> Int -> Person

Basically, it takes values for the name and the age and gives us a fully fledged person. Great!

record Person =
    name : String,
    age  : Int,

func main : IO =
    let (Person "Joe" 28) \joe
    quit

We've got Joe! How do we use him?

In addition to the constructor function, Funky generates two functions per field: a getter and an updater. Name of both of the functions is the same as the name of the field:

$ funkycmd -types person.fn
> name
Person -> String
(String -> String) -> Person -> Person

The type Person -> String is the getter. It works just as you'd expect:

record Person =
    name : String,
    age  : Int,

func main : IO =
    let (Person "Joe" 28) \joe
    println (name joe);
    quit

Running it:

$ funkycmd person.fn
Joe

The updater with the type (String -> String) -> Person -> Person is a little more... funky.

Here's what it does: it takes a function and a person. It returns a new person that is the same as the old one, except with the field modified by the function.

Let's see:

record Person =
    name : String,
    age  : Int,

func main : IO =
    let (Person "Joe" 28)       \joe
    let (name (++ ", yo!") joe) \joe  # shadows the previous joe variable
    println (name joe);
    let (age (+ 1) joe) \joe          # Joe had a birthday!
    println (string; age joe);
    quit

And run it:

$ funkycmd person.fn
Joe, yo!
29

Note. If you want to replace the field's value by some other value, you can use the const function like this: name (const "Joseph") joe (changes the name to "Joseph"). The function const makes a function that, taking any input, always evaluates to a constant. So, (const "Joseph") 12 evaluates to "Joseph".

The signatures of the getters and the updaters are not random. They enable some really cool stuff! We'll check it out now.

I'll show it to you on these two records:

record Point =
    x : Int,
    y : Int,

record Line =
    from : Point,
    to   : Point,

Okay, now, say we have a Point, let's call it pt. To get the X coordinate we do x pt and to get the Y coordinate we do y pt. Easy! To move the X coordinate 10 units to the right, we do x (+ 10) pt and to set the Y coordinate to 0 we do y (const 0) pt.

Okay, now say we have Line. Let's call it line. The line has two points: from and to. What if we want to move the X coordinate of the first point by 10?

Now, here comes the cool part! All we need to do it to realize, that

x (+ 10)

is a partial application of the x updater and has type Point -> Point. But, any Point -> Point can be used in the from updater:

from (x (+ 10)) line

Lastly, we can clean it up with the function composition operator:

(from . x) (+ 10) line

Note. The function composition operator . works like this: (f . g) x = f (g x). So you see we've just rewritten the previous expression using this formula.

Details. In Funky, the function composition operator is overloaded a few times in the standard library, namely for when the second function takes multiple arguments. For example, one of the overloaded versions works like this: (f . g) x y = f (g x y). That way, writing (concat . map) works exactly as you'd like to. The type checker can always tell which version fits the context.

And that's it! That's pretty clean, isn't it?

Getters can be composed similarly, except in the opposite order:

(y . to) line

That's the Y coordinate of the last point.

Getters and updaters also have a very important role when it comes to expressing state flow with the State type as we'll cover in the part about expressing imperative algorithms. In short, they enable record fields to act as mutable variables in an imperative algorithm.

The second way of creating new types is unions. While a record is a collection of fields, a union defines multiple alternative forms.

Here's the general form:

union Name = alternative argument ... | ...

The three dots after argument mean that a single alternative can contain any number of arguments (fields) and the three dots after | mean that a union can have any number of alternatives.

Unlike records, arguments for alternatives have no names, only types.

Here's a simple union:

union Bool = true | false

This is the actual definition of the type Bool from the standard library. The alternatives have no arguments in this case.

Here's another example:

record Point = x : Float, y : Float

union Shape =
    line Point Point   |
    circle Point Float |

Note. Trailing | is allowed.

The Shape type has two alternatives: the line alternatives, which is composed of two points, and the circle alternatives, which has a point (the center) and a float (the radius).

When we define a union, Funky generates a constructor function for each alternative. The function simply takes all the arguments in order. Let's check them out!

$ funkycmd -types shapes.fn
> line
Point -> Point -> Shape
> circle
Point -> Float -> Shape
> line (Point 1.0 8.0) (Point 12.5 -4.9)
Shape
> circle (Point 0.0 0.0) 7.0
Shape

They definitely work!

To examine a Shape value and make a decision based on whether it's a line or a circle, Funky provides the switch/case construct. It's best shown by an example. Here's a function that calculates the length of a line or a circumference of a circle:

func length : Shape -> Float =
    \shape
    switch shape
    case line \from \to
        hypot (x to - x from) (y to - y from)
    case circle \center \radius
        2.0 * pi * radius

Note. The hypot function stands for 'hypotenuse' and is used for calculating the length of the long side of a right triangle using the Pythagorean theorem: hypot x y = sqrt ((x ^ 2.0) + (y ^ 2.0)).

As you can see, the switch/case construct begins with the switch keyword followed by the value we're switching on. After that, we see a series of case branches. Each branch starts with the case keyword followed by the name of the alternative. That is followed by a function that takes the arguments to the alternative and evaluates to the overall result.

Of course, all case branches must evaluate to the same type: Float, in our case.

Note. Currently, all alternatives must be present in switch/case and they must be listed in the same order as they are in the definition of the union. This will be fixed.

The names of the alternatives can also be infix if they don't contain any letters. When they are infix, they can be placed between their arguments in the definition.

For example, here's a nice, recursive union for building up arithmetic expressions:

union Expr =
    num Int     |
    Expr + Expr |
    Expr * Expr |

It's either just a number, like num 12, or it's an addition, or a multiplication: num 12 + num 7, or (num 1 + num 9) * ((num 4 + num 3) + (num 2 * num 2)).

Note. The alternatives can be called + and * without a problem thanks to overloading.

To evaluate an expression like that, we make use of switch/case again:

func eval : Expr -> Int =
    \expr
    switch expr
    case num
        self
    case (+) \left \right
        eval left + eval right
    case (*) \left \right
        eval left * eval right

Have you noticed that no lambda comes after case num? That's because the case bodies need not explicitly contain lambdas, all they need is a function. In this case, self (the identity function) is the right choice because it just evaluates to the number under num.

Let's see if eval works right!

union Expr =
    num Int     |
    Expr + Expr |
    Expr * Expr |

func eval : Expr -> Int =
    \expr
    switch expr
    case num
        self
    case (+) \left \right
        eval left + eval right
    case (*) \left \right
        eval left * eval right

func main : IO =
    let ((num 1 + num 9) * ((num 4 + num 3) + (num 2 * num 2))) \expr
    println (string; eval expr);
    quit

And run it:

$ funkycmd expr.fn
110

Works great!

So far we've only defined types that were concrete, with no type variables anywhere. But it's also possible (and very useful) to define generic types: types parameterized by one or more type variables.

It's really simple.

All we need to do is to list the type variables after the name of the type in the definition:

record Pair a b =
    first  : a,
    second : b,

That's an actual definition of the Pair type from the standard library.

Or here's another example:

union Maybe a = none | some a

That is, likewise, the definition of the Maybe type from the standard library.

This way, Pair and Maybe don't define a single type each. Instead, each defines a family of types: Pair Int Float, Pair String Bool, Maybe (String -> String), Maybe (Pair Int Int) all belong to those families.

Note. 'Type family' is not a concept in Funky, it's just a phrase we use to talk about types. Pair without its type variables filled in is always an error.

Aliases are sooo simple! Too simple. All they do is they define a new name for an existing type:

alias Name = type

That's it!

The String type is an alias:

alias String = List Char

Therefore, String and List Char are perfect synonyms.

Of course, aliases can also contain type variables and have one interesting, although not very useful feature: they can be recursive. I haven't found a situation yet where a recursive alias would be needed, but I'll leave that up to you. ;)

If you've read everything up until this point in the tour, you know the whole language! Does it feel like it? Probably not. The language itself feels kinda empty. There isn't much there. You can make functions, types, apply functions, and well, that's about it.

Now, we'll learn how these simple building blocks are put together to build "the rest of the language" in the standard library.

Lists. They are the butter and bread of functional programming and possibly my favorite data structure ever.

This is how they are defined in the standard library:

union List a = empty | a :: List a

It's a trivial linked list, which means you can't access elements randomly, you always have to traverse them in order.

As you can see, lists can either be empty or have a first element and a rest of the list. Using the :: constructor repeatedly allows for creating longer and longer lists:

empty
1 :: empty
1 :: 2 :: empty
1 :: 2 :: 3 :: 4 :: 5 :: 6 :: 7 :: empty

And using recursion, one can even create infinite ones:

func one-two-three : List Int = 1 :: 2 :: 3 :: one-two-three

This doesn't enter an infinite loop because Funky is a lazily evaluated language.

Of course, typing colons all the time would be tiresome, and so Funky provides a nice syntax sugar with the usual square brackets.

["a", "b", "c", "d"]

Expands to:

"a" :: "b" :: "c" :: "d" :: empty

Well, actually... since the String type is defined as List Char, the string literals must also get expanded to colons, right? Yep, so the full expansion actually is this monstrosity:

('a' :: empty) :: ('b' :: empty) :: ('c' :: empty) :: ('d' :: empty) :: empty

After seeing this, I'm sure you're way more grateful for all the string and list syntax sugar than you've ever been before.

With lists comes the legacy of tools, perfected and sharpened for long generations.

The most basic and important ones are empty?, first! and rest!:

$ funkycmd -types
> empty?
List a -> Bool
> first!
List a -> a
> rest!
List a -> List a

The REPL will print more version of the empty? function, but the one listed here is the important one. The functions are simple: empty? tells if a list is empty, first! returns the first element of the list, and rest! cuts off the first element and returns what remains. All other list functions can be implemented in terms of these three (or in terms of switch/case).

Details. Functions first! and rest! have the '!' symbol in them because they can crash: they crash when the list is empty. They have their non-crashing versions called first and rest that return a Maybe. We'll learn more about maybes in another part.

Now, let me (re)introduce you to map and filter.

The function map simply applies a function to all of the elements of the list:

map sqrt [1.0, 4.0, 9.0, 16.0]  # => [1.0, 2.0, 3.0, 4.0]
map (* 3) [5, 1, 3, 2]          # => [15, 3, 9, 6]

The function filter takes a predicate and filters out all the elements that don't satisfy it:

filter (< 5) [9, 3, 4, 7, 5, 10, 1]  # => [3, 4, 1]
filter even? [1, 2, 3, 4, 5, 6, 7]   # => [2, 4, 6]

Then there is a nice zip function which "zips" two lists with some binary function (it's like zipWith from Haskell; the zip function from Haskell can be done with zip pair in Funky). It takes the first elements from both lists, applies the function to them, and goes on, like this:

zip (*) [1, 2, 3] [2, 3, 4]           # => [2, 6, 12]
zip (++) ["he", "wo"] ["llo", "rld"]  # => ["hello", "world"]

The zip function enables this ultra cool hipster Fibonacci one-liner:

func fibs : List Int =
    0 :: 1 :: zip (+) fibs (rest! fibs)

There are more list functions, like fold< and fold> (those are same as foldr and foldl' in Haskell), but we'll not give them too much attention, you can try them out on your own. For example, here's how you'd sum a list of numbers with fold>:

fold> (+) 0 (range 1 15)  # => 120

Other list functions include reverse, take, drop, any, all, iterate, and so on. The usual ones.

Now, all that stuff is cool, but if we can't print a list, it's all useless, right? Well, this leads us to a very interesting function from the standard library called for. Yes, the name is intentionally chosen to match the name of the old imperative concept - the for-loop. Of course, loops in imperative programming rely on the mutation of the loop variables. We can't do that in functional programming, but our for-loop will be just as ergonomic as the imperative one.

So, what's the type of this mighty for function?

$ funkycmd -types
> for
List a -> (a -> c -> c) -> c -> c

It takes three arguments. Here's what they are and how you can think about them:

• List (type List a). This is the list of things we want to loop over.
• Body (type a -> c -> c). You can think of this as something we want to "do" for each element.
• Next (type c). This will get "done" after getting over with all the elements.

Obviously, the descriptions above are rather inaccurate. We can't do anything, we can only make values and data structures.

The best way to explain what for does is to start with an example. So, let's print a list:

func main : IO =
    for ["A", "B", "C"]
        println;
    quit

Oh man, that looks imperative! Does it even work?

$ funkycmd for.fn
A
B
C

It does!

We've passed ["A", "B", "C"] as the list to for. Then we passed println as the body. The println function perfectly fits the required type of the argument: a -> c -> c, specialized to String -> IO -> IO in our case. Because println takes and returns IO, the last argument to for must be an IO. So we passed quit.

As we already know, println constructs the IO data structure and the same goes for quit. So for is in fact just applying functions in some way. What could that way be?

First of all, if we pass an empty list, we just get the next back.

for [] body next  # => next

If we pass a single element list, we get the body applied to the element and the next:

for [a] body next  # => body a next

What about a two element list? Well, that looks like this:

for [a, b] body next  # => body a (body b next)

Three elements?

for [a, b, c] body next  # => body a (body b (body c next))

In other words:

for (x :: xs) body next

is equivalent to:

body x (for xs body next)

which can be easily rewritten to:

body x;
for xs body;
next

The working of for can also be seen in the following diagram:

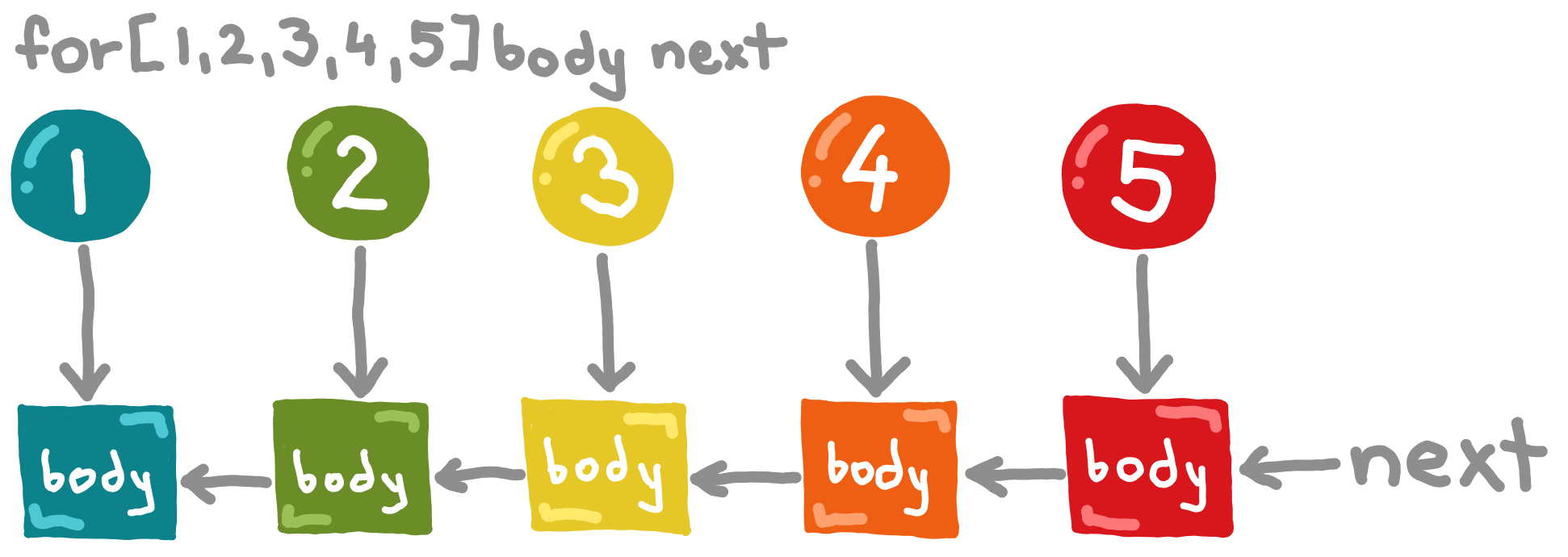
Note. Yes, for is exactly the same function as fold<, except with a different order of arguments.

Knowing this, it's easy to see that our list printing program:

func main : IO =
    for ["A", "B", "C"]
        println;
    quit

basically expands to this:

func main : IO =
    println "A";
    println "B";
    println "C";
    quit

It's all very clear now!

The next argument doesn't have to be just a quit. It can be more complex:

func main : IO =
    for ["A", "B", "C"]
        println;
    println "Done!";
    quit

or even another for loop:

func main : IO =
    for ["A", "B", "C"]
        println;
    println "First half!";
    for ["D", "E", "F"]
        println;
    println "Second half!";
    quit

With the semicolon, we can get much of the convenient code structuring of imperative programming. Without monads!

If we change the list to a list of numbers, the scheme no longer works:

func main : IO =
    for (range 1 5)
        println;
    quit

Details. The range function takes the lower and the upper bound and evaluates to a list of all integers in between, including the bounds.

Trying to run this gives us an error:

$ funkycmd for.fn
for.fn:3:9: type-checking error

That's quite obvious. We have a list of Ints, but println takes a String. This can be fixed by composing println with string, which converts Ints (and is overloaded for other types) to Strings:

func main : IO =
    for (range 1 5)
        (println . string);
    quit

This time, it works!

$ funkycmd for.fn
1
2
3
4
5

So far, we've only seen a simple function or a composition of two functions as the body argument to for. What if we want to have a more elaborate loop body? Say a two printlns for the start.

You might be tempted to try this:

func main : IO =
    for (range 1 5)
        (print "#"; println);
    quit

But that just doesn't work. We can't pass println as the second argument to print, that's just nonsense, it expects an IO, not String -> IO -> IO.

Here's what we need to do. Let's start with the simple for-loop on strings.

func main : IO =
    for ["A", "B", "C"]
        println;
    quit

Instead of just passing the function println itself, let's make it a lambda:

func main : IO =
    for ["A", "B", "C"] (
        \s \next
        println s;
        next
    );
    quit

The body of the for loop takes two arguments: the element of type String, and the continuation of type IO. We pass both of these to the println function, recreating the original, short for-loop. This doesn't at all change the behavior of the program.

However, as you can surely see, it's very straightforward to add more "statements" to the body:

func main : IO =
    for ["A", "B", "C"] (
        \s \next
        print "- ";
        println s;
        next
    );
    quit

Let's run it!

$ funkycmd body.fn
- A
- B
- C

We can even add scans to the loop!

func main : IO =
    print "What's the number of questions? ";
    scanln \n-str
    let (int n-str) \n
    for (range 1 n) (
        \i \next
        print ("Your question #" ++ string i ++ ": ");
        scanln \question
        println "The answer: IDK.";
        next
    );
    quit

Let's run this funny program:

$ funkycmd questions.fn
What's the number of questions? 3           
Your question #1: What's your name?
The answer: IDK.
Your question #2: How are you doing IDK?
The answer: IDK.
Your question #3: Do you know anything?
The answer: IDK.

And you can even nest loops! Here's a program that prints out the small multiplications table... in a non-tabular form, but that's okay.

func main : IO =
    for (range 1 10) (
        \x \next
        for (range 1 10) (
            \y \next
            print (string x);
            print " x ";
            print (string y);
            print " = ";
            println (string (x * y));
            next
        );
        next
    );
    quit

Note. Those multiple prints aren't necessary, it could've all been done with one long string concatenation. Splitting it into multiple lines just makes it clearer. This problem will go away once there is a better way to format strings.

And run it!

$ funkycmd multiplications.fn
...
5 x 7 = 35
5 x 8 = 40
5 x 9 = 45
5 x 10 = 50
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
...

It works! I didn't show the whole output, because that's too large, but you get the idea.

That's it for this part, in the next part, we'll learn more list tricks!

You thought the vertical code was just for IO? You were wrong! Vertical code (the one that spans vertically and can be read top to bottom) is quite universal in Funky. In this part, we'll see how it can be applied to lists and their generation.

The basic list constructor, the double colon, is an infix function. That makes it unusable for vertical code. However, the standard library defines a synonym of :: called yield:

func yield : a -> List a -> List a = (::)

It's a literal synonym. But, it's a prefix function. How does that help?

Take this list:

[1, 2, 3]

Rewrite it with the colons:

1 :: 2 :: 3 :: empty

Cool. Now, how would this look if we used yield instead?

yield 1 (yield 2 (yield 3 empty))

All we did was replace all ::s with yields. And here it comes. Can you see it? We can use the semicolon and make it vertical!

yield 1;
yield 2;
yield 3;
empty

Beautiful!

To get to know yield a little better, let's use it to rewrite some well-known functions. How would the map function look like using yield? Something like this:

func my-map : (a -> b) -> List a -> List b =
    \f \list
    for list (
        \x \next
        yield (f x);
        next
    );
    empty

The for function isn't just for IO. It can be used with anything that composes vertically. We take the function f and the list and we yield all of its elements in order, except we transform them with f.

We can even make the code shorter with function composition:

func my-map : (a -> b) -> List a -> List b =
    \f \list
    for list (yield . f);
    empty

That's really nice.

How would filter look like with yield? In the case of filter, we can't yield all the elements of the list. We must only yield those that satisfy the predicate. That's where the when function comes handy:

$ funkycmd -types
> when
Bool -> (a -> a) -> a -> a

It's kinda similar to if, but different. While if chooses between two alternatives, when conditionally applies its second argument (the body) to the third (the next). Specifically, when works like this:

when true body next   # => body next
when false body next  # => next

For example:

when (x > 7) (1 +) x

This expression evaluates to x + 1 if x is more than 7, otherwise, it evaluates to x.

So, let's use when to implement my-filter!

func my-filter : (a -> Bool) -> List a -> List a =
    \p \list
    for list (
        \x \next
        when (p x) (yield x);
        next
    );
    empty

That's it! Here, we can't easily compress the loop body into some stunning composition, but so what. It isn't that bad anyway.

Structuring list generation vertically comes very handily when dealing with complex list generating functions. One of the best examples is a function to format lists so that we can print them with one println. Such a function isn't currently present in the standard library. But we'll make our own!

First, we gotta choose the type. What could it be? Perhaps this one?

List a -> String

Well, this is what it will be in the future when the with clause gets implemented, but so far, we can't do it that way. Why? We're accepting List a: a list of any type. To convert it to a string, we need to convert each of its elements to a string. But, there's no general way of converting an arbitrary type to string - the string function is only implemented for a handful of types.

This will do:

(a -> String) -> List a -> String

In addition to the list itself, we'll accept a function that helps us convert the elements to strings. Okay, let's get to the code!

func list->string : (a -> String) -> List a -> String =
    \str \list
    # TODO

The type String is an alias for List Char - the list of characters. That's what we have to produce. We start with the opening square bracket:

func list->string : (a -> String) -> List a -> String =
    \str \list
    yield '[';
    # TODO

Now we have to loop over the list and yield the string versions of the elements. We also gotta put commas between them. We gotta put a comma before each element except the first one. How are we going to achieve that?

We'll learn two more functions: enumerate and for-pair. The enumerate function takes a list and adds an index to each element. Its type is List a -> List (Pair Int a). For example: enumerate ["A", "B", C"] evaluates to [pair 0 "A", pair 1 "B", pair 2 "C"]. You get the idea. Now, for-pair lets us easily iterate over a list of pairs. It's just like for, but it's body function takes two elements instead of one - for-pair unpacks the pairs.

func list->string : (a -> String) -> List a -> String =
    \str \list
    yield '[';
    for-pair (enumerate list) (
        \i \x \next
        # TODO
    );
    # TODO

The i variable is the index, the x variable is the original element from list. If the index is zero, we know we're dealing with the first element and we won't add the comma. Otherwise, we'll add it.

func list->string : (a -> String) -> List a -> String =
    \str \list
    yield '[';
    for-pair (enumerate list) (
        \i \x \next
        when (i > 0) (yield-all ", ");
        yield-all (str x);
        next
    );
    # TODO

What's that yield-all? It's just like yield, but it yields a whole list of things, instead of just one element. It's a synonym for ++. In general:

yield-all list;
next

is equivalent to:

for list yield;
next

All that remains now is finishing with the closing square bracket:

func list->string : (a -> String) -> List a -> String =
    \str \list
    yield '[';
    for-pair (enumerate list) (
        \i \x \next
        when (i > 0) (yield-all ", ");
        yield-all (str x);
        next
    );
    yield ']';
    empty

And we're done! It's so nice and readable having this function expressed vertically.

Note. Actually, list->string can be done nicer in a functional style using the join function.

"[" ++ join ", " (map str list) ++ "]"

Functional solutions are often superior to imperative ones. We've done list->string imperatively just for the demonstration.

Let's test it out! We'll print all the primes until 100. First, the prime testing function:

func prime? : Int -> Bool =
    \n
    all (\x not zero?; n % x) (range 2 (n - 1))

It simply tests whether no number between 2 and n-1 divides n. The % sign is the modulo operator. Now we'll make an infinite list of primes:

func primes : List Int =
    filter prime? (iterate (+ 1) 2)

Details. The function iterate successively applies the provided function to the provided initial value producing an infinite list of all the results. In our case, iterate (+ 1) 2 produces [2, 3, 4, 5, 6, ...]. For example, iterate (* 2) 1 would produce [1, 2, 4, 8, 16, 32, ...].

Okay, now, let's print them up to 100:

func main : IO =
    let (take-while (< 100) primes) \primes<100
    println (list->string string primes<100);
    quit

Details. The take-while function is different from filter. While filter takes all the elements that satisfy a predicate, take-while takes elements from the list, but stops taking them the moment it encounters the first element to not satisfy the predicate. That's important here. Had we used filter, the program wouldn't halt. It would continue searching the infinite list of primes for another element less than 100, but it would never find one. Using take-while makes the program halt because we never search beyond the first wrong one.

Let's run it!

$ funkycmd primes.fn
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

Works like charm!

In the next part, we'll learn how to express state flow. Things will get really imperative... in a purely functional way.

Sometimes, the best way to express a function is by a series of state-changing steps. In other words, by an imperative algorithm. For example, say we want to reverse a list. That's a fairly common thing. Sure, we could use the reverse function from the standard library, but how can we make one ourselves?

Here's a way to make it happen:

1. Have two variables: left and right.
2. Store the input list in the left variable.
3. Store an empty list in the right variable.
4. Repeat until the left list is empty:
   1. Add the first element of the left list to the beginning of the right list.
   2. Remove the first element from the left list.
5. Output the right list.

For example, let's try and reverse [1, 2, 3, 4, 5]. Here's how the algorithm would proceed:

           left | right
[1, 2, 3, 4, 5] | []
   [2, 3, 4, 5] | [1]
      [3, 4, 5] | [2, 1]
         [4, 5] | [3, 2, 1]
            [5] | [4, 3, 2, 1]
             [] | [5, 4, 3, 2, 1]

At the end, the left list is empty and the right list contains the reversed version of the original input list.

Note. Adding/removing an element to/from the beginning of a list is efficient (constant time). The whole algorithm, therefore, runs in time linearly proportional to the size of the list.

How could we implement such an algorithm in Funky?

Well, this one isn't particularly hard. We can utilize recursion to simulate the state flow. We create a function called my-reverse-algo, which has two arguments: left and right. Those represent the two variables used in the algorithm. If the left list is empty, my-reverse-algo simply returns the right list. Otherwise, it returns from a recursive call with the variables updated appropriately.

func my-reverse-algo : List a -> List a -> List a =
    \left \right
    if (empty? left) right;
    my-reverse-algo (rest! left) (first! left :: right)

Details. In most languages, each recursive call would grow the stack and we would quickly run out of memory. This doesn't happen in Funky thanks to tail recursion. If a function should evaluate directly to another function call, it simply jumps to that function, effectively creating an efficient loop.

Now we'll use my-reverse-algo to implement my-reverse. It'll just pass the correct initial values to my-reverse-algo:

func my-reverse : List a -> List a =
    \list
    my-reverse-algo list []

Let's see if it works!

func main : IO =
    for (my-reverse [1, 2, 3, 4, 5])
        (println . string);
    quit

And run it:

$ funkycmd my-reverse.fn
5
4
3
2
1

Nice!

Could we somehow get rid of the helper my-reverse-algo function? It isn't really useful on its own, it's just an implementation detail. It shouldn't be there.

What would help would be some way to define recursive functions anonymously, i.e. without making a global func definition. That way we could define my-reverse-algo directly inside my-reverse.

The function for this job is called recur, otherwise known as the fixpoint combinator, or the Y combinator. It's a pretty mind-blowing function. I won't explain how it works (it took me a long time to figure it out), but I'll explain how you can use it.

Here's the type, but it won't help you figure out much:

$ funkycmd -types
> recur
(a -> a) -> a

Okay, so how to use it? Let's take this really simple recursive function:

func ones : List Int = 1 :: ones  # [1, 1, 1, ...]

It isn't even a function, it's just a recursive list.

We can express the same recursive list using recur like this:

recur \ones 1 :: ones

The variable ones isn't a global definition, in this case, it's just a local binding. Does it work?

func main : IO =
    for (take 5; recur \ones 1 :: ones)
        (println . string);
    quit

We only take the first five elements, because the list is infinite.

$ funkycmd ones.fn
1
1
1
1
1

It does work!

What about this function?

func count-from : Int -> List Int =
    \x x :: count-from (x + 1)

For example, count-from 4 evaluates to [4, 5, 6, 7, ...].

With recur, it looks like this:

recur \count-from \x
x :: count-from (x + 1)

You can try it yourself. Remember, that this time it's a function with one argument, so you need to pass it in.

So, I guess you got it, right? To define an anonymous recursive function, simply type recur and pass it a lambda where the first argument acts as the name of the recursive function and the rest are its arguments. Simple as that.

What about Fibonacci?

recur \fibs \a \b
a :: fibs b (a + b)

This defines a function that given two initial numbers produces a Fibonacci-like sequence. If we give it 0 and 1 as the initial numbers, it will produce the Fibonacci sequence precisely:

(recur \fibs \a \b
a :: fibs b (a + b)) 0 1

Have you noticed them? The 0 and 1 that we passed in. They are right there, at the end of the expression. Perhaps you saw them, perhaps you didn't, but you surely must admit that it doesn't look very fashionable.

Instead of simply passing the arguments like usually, we can use the |> function to pass them. It works like this:

x |> f

is the same as:

f x

So, with |>, we can rewrite the previous expression like this, but we need to pass the arguments in seemingly reverse order:

1 |> 0 |> recur \fibs \a \b
a :: fibs b (a + b)

Explanation. The above code works, we pass 0 for a and 1 for b, not the other way around. This is because y |> x |> f is the same as y |> (x |> f), which reduces to y |> f x, and finally f x y.

This whole expression evaluates to just [0, 1, 1, 2, 3, 5, 8, 13, 21, ...], the infinite Fibonacci sequence.

I admit, the whole thing about passing the arguments in seemingly reverse order may look kinda confusing to you, but don't worry, you'll get used it. It's very versatile, and the whole thing didn't require a single language addition.

Can we use recur to get rid of the extra my-reverse-algo function?

For the reminder, here's how it looks with the extra function:

func my-reverse-algo : List a -> List a -> List a =
    \left \right
    if (empty? left) right;
    my-reverse-algo (rest! left) (first! left :: right)

func my-reverse : List a -> List a =
    \list
    my-reverse-algo list []

And here's the solution. All we have to do is replace my-reverse-algo in the body of my-reverse with an anonymous definition:

func my-reverse : List a -> List a =
    \list
    (recur \my-reverse-algo \left \right
    if (empty? left) right;
    my-reverse-algo (rest! left) (first! left :: right)) list []

And we'll use |> to make it more readable:

func my-reverse : List a -> List a =
    \list
    [] |> list |> recur \my-reverse-algo \left \right
    if (empty? left) right;
    my-reverse-algo (rest! left) (first! left :: right)

The last change we'll make is we'll rename my-reverse-algo to simply loop:

func my-reverse : List a -> List a =
    \list
    [] |> list |> recur \loop \left \right
    if (empty? left) right;
    loop (rest! left) (first! left :: right)

This is a little convention. In cases like this, we choose loop as the local name of the recursive function. It makes it immediately clear that we're using recur to simulate a simple stateful loop.

Sometimes, simple loops like the above aren't powerful enough. Of course, we prefer them whenever possible. But some algorithms require a more nuanced expression.

A good example is the imperative version of the quicksort algorithm, i.e. quicksort on random-access arrays. That's a little too tough for the start, but we'll come back to it by the end of this part.

First, we need to learn how to express imperative algorithms. The standard library offers a type specifically for this purpose: Proc. That's short for procedure. It's a simple union with this definition:

union Proc s r =
    view (s -> Proc s r)       |
    update (s -> s) (Proc s r) |
    return r                   |

Note. Proc is an equivalent of the State monad from Haskell and was initially called the same.

So, what's Proc all about? You can think of it as a description of a procedure that runs in some stateful context, (usually) changes it, and results in some return value. Let's take a close look!

First, it has two type variables:

• s. This is the type of the state context the procedure will run in. For example, if s is Int, then the procedure will begin its execution with some initial Int, say 4, be able to change it and check its current value during its execution.
• r. This is the return type. When a procedure finishes, it returns some value, just like procedures in imperative languages.

Second, it's a union with three alternatives or commands:

• view. Used to check the current value of the state. Notice that its signature resembles the signature of scanln and similar functions. It's used the same way.
• update. This one is used to change the state. It takes a function of type s -> s. When executing the procedure, the current state will be mapped through this function. The second argument is a continuation - tells what should be done next. The update function is used in the same way as println and similar functions.
• return. Marks the end of the procedure and specifies the return value.

Using these three instructions together with our already acquired battle-tested tools, like if and for, we can make descriptions of stateful procedures.

Let's see that in action!

Our first trivial example will be a procedure whose state context is just an Int and which returns an Int as well. When executed, it will increment the number in the state by 1 and return its new value.

func increment : Proc Int Int =
    update (+ 1);
    view \x
    return x

First, we update the state using (+ 1) (which is the same as (\x x + 1)). Then we get the current (updated) state and return it.

The return function has an overloaded version:

func return : (s -> r) -> Proc s r =
    \f
    view \x
    return (f x)

It takes the current state and makes a return value from it using the supplied function. In our case, we just want to return the state directly, so we'll use self (which is the identity function: \x x):

func increment : Proc Int Int =
    update (+ 1);
    return self

That's quite neat! Now, keep in mind, all we have constructed is a data structure - a description. How do we execute it?

We need to provide some initial state value. The function start-with is for just that. Here's how it looks like:

func start-with : s -> Proc s r -> r

It takes the initial state, then a procedure, and apparently it executes the procedure and evaluates to its return value. Let's see how that works!

func main : IO =
    let (start-with 6 increment) \x
    println (string x);
    quit

And run this:

$ funkycmd increment.fn
7

What if we want to execute increment multiple times? We can do that using the call function:

func call : Proc s a -> Proc s b -> Proc s b

This function is used for executing one procedure inside another procedure, discarding the return value of the first (we are able to get it, just wait a moment).

It takes two procedures and produces a new procedure that executes them one after another, returning the result of the second one.

func main : IO =
    let (start-with 6 (call increment increment)) \x
    println (string x);
    quit

Does it work?

$ funkycmd call.fn
8

Yep, it works! We can even reorganize it horizontally:

func main : IO =
    let (
        start-with 6;
        call increment;
        increment
    ) \x
    println (string x);
    quit

We could even increment four times!

func main : IO =
    let (
        start-with 6;
        call increment;
        call increment;
        call increment;
        increment
    ) \x
    println (string x);
    quit

The call function has another version with this type:

func call : Proc s a -> (a -> Proc s b) -> Proc s b

It's the same as the first version, except that instead of taking just a procedure as the second argument, it accepts a function taking the return value of the first procedure. The usage is quite straightforward.

Just for fun, let's gather all the return values from those three increments using this new call version and return their sum:

func main : IO =
    let (
        start-with 6;
        call increment \x
        call increment \y
        call increment \z
        return (x + y + z)
    ) \w
    println (string w);
    quit

What will be the result?

$ funkycmd call.fn
24

That's because 7+8+9=24.

Imperative algorithms usually work with multiple variables.

For example, a simple algorithm to accumulate an average of a stream of numbers must store two variables: the sum and the count. The final average is then obtained by dividing one by the other. To add a number to the average, we add it to the sum and we increase the count by 1.

A natural way to store these two variables in Funky is with a record:

record Average =
    sum   : Int,
    count : Int,

Then, using the record accessors, we can make a procedure to add a number to the average:

func add : Int -> Proc Average Nothing =
    \number
    update (sum (+ number));
    update (count (+ 1));
    return nothing

We use the Nothing return type, which is a type with only a single possible value: nothing. We use it to denote a procedure with no (useful) return value.

Note. Nothing is the same type as () in Haskell or Unit in some other languages.

This isn't so bad. But, trust me, writing update (field ...) over and over gets tiresome with longer procedures. Records are so frequent here that the standard library provides some special treatment for them.

The first function for this purpose is <-. It's used to change a record field (or a nested field) in a procedure. Whenever you write this:

update (field function)

you can instead rewrite it to this:

field <- function

Note. The <- function has type ((a -> a) -> s -> s) -> (a -> a) -> Proc s r -> Proc s r.

Therefore, we can rewrite our add function into this beautiful piece of code:

func add : Int -> Proc Average Nothing =
    \number
    sum <- + number;
    count <- + 1;
    return nothing

Pretty cool, don't you think?

Another useful function is ->. On the left side, it takes a getter, a function from the state type. Then it passes its result to the lambda on the right. It's like an enhanced view - whereas view always gives back the entire state, -> gives you the part of the state you request.

For example, how about a procedure that returns the actual current average as an Int?

func average : Proc Average Int =
    sum -> \s
    count -> \c
    return (if (zero? c) 0 (s / c))

Simple as that. We make sure to handle the case when the count is 0 using if as a ternary operator.

Using add and average, we can compose an imperative algorithm for calculating the average of a list:

func average : List Int -> Int =
    \numbers
    start-with (Average 0 0);
    for numbers (call . add);
    call average \avg  # call to the procedure, not a recursive call
    return avg

Note. We overloaded the name average for two purposes here: one is the procedure and the other is the function. No worries, Funky can always tell the difference.

Notice that this average function has no Proc in the type. All the procedure stuff is encapsulated inside of it. To the outside world, it appears simply as another function.

The last function for working with records in procedures is :=. It's similar to <-, but instead of transforming the original value using a function, it simply overwrites it with a new value.

In other words, you can always replace this:

field <- const value

with this:

field := value

Say we wanted to reset the average counter. Here's what it would look like:

func reset : Proc Average Nothing =
    sum := 0;
    count := 0;
    return nothing

Details. There's an overloaded version of := which takes a function from the state instead of a direct value. It can be used to copy one part of the state into another. We could, for example, write: sum := count, even though that wouldn't make any sense. But, be careful. You can't write sum := count * 2, because count is a getter (a function) here, not a number. You could write sum := (\s count s * 2), though.

By the way, the function self acts as both a getter and an updater for the whole state. Remember this function?

func increment : Proc Int Int =
    update (+ 1);
    return self

We can rewrite it:

func increment : Proc Int Int =
    self <- + 1;
    return self

Yes, this usage was one of the motivations for naming it self instead of id.

The last piece of the puzzle before we can finally implement the quicksort algorithm is random-access arrays.

Arrays in Funky are a bit different than arrays in imperative languages because we aren't allowed to mutate anything. To change an element in an array we must make a new array. But no full copies need to be performed. The new array can always share as much data as possible with the old one and thus the whole operation will be quite cheap.

Details. Without cheating, there's really no such thing as in-place, mutable, O(1) access arrays in purely functional programming. All data structures have to be primarily tree-based and persistent.

However, there are efficient ways of implementing persistent arrays with O(log n) access time.

Currently, the Array type in Funky implements an infinite array indexed by Ints (both positive and negative). To create an empty array, we use the empty function:

func empty : a -> Array a

It takes one argument, which is the default initial value for all elements. For example:

empty 0

is an Array Int full of zeros. We use at to both get and update any element in the array. Here are the two overloaded versions:

func at : Int -> Array a -> a
func at : Int -> (a -> a) -> Array a -> Array a

As you have surely noticed, they look very similar to getters and updaters in records, except that they take an additional Int argument - the index. For example:

at 5 array

gets the element at the index 5, while:

at 5 (+ 3) array

evaluates to a new array, where that element is increased by 3.

There are two more functions, namely reset and swap. We won't cover the first one, but we'll come back to the second one when we get to the quicksort.

That's basically all there is to arrays. The interesting part comes when integrating them with procedures.

As we've already noticed, both version of at fit very well with the form of record accessors. And we can, in fact, use them the same way in procedures. For example:

func some-array : Array Int =
    start-with (empty 0);
    at 0 := 7;
    at 1 := 4;
    at 2 := 9;
    at 3 := 5;
    at 4 := 2;
    return self

func main : IO =
    for (range 0 4) (
        \i \next
        println (string; at i some-array);
        next
    );
    quit

We manually assign values to the elements of an array. Then, in main, we loop over the indices from 0 to 4 and print the corresponding elements from the array. Does it work?

$ funkycmd array.fn
7
4
9
5
2

Sure enough, it does!

We can even shorten some-array with a for-loop:

func some-array : Array Int =
    start-with (empty 0);
    for-pair (enumerate [7, 4, 9, 5, 2])
        (\i \x at i := x);
    return self

Now that we know arrays, let's get on to the quicksort!

If you've ever implemented quicksort, you must know that it's quite tricky to get it right unless you're a super brilliant genius. At least the first time.

Because of that, we'll make our job easier and simply translate this algorithm from Wikipedia:

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p := partition(A, lo, hi)
        quicksort(A, lo, p - 1)
        quicksort(A, p + 1, hi)

algorithm partition(A, lo, hi) is
    pivot := A[hi]
    i := lo
    for j := lo to hi - 1 do
        if A[j] < pivot then
            swap A[i] with A[j]
            i := i + 1
    swap A[i] with A[hi]
    return i

That's pseudocode. We'll try and translate it to Funky. We'll make two procedures: quicksort and partition.

Since these are imperative, we'll need the array in their mutable state. The partition procedure also uses an index i, so we'll also need that in the state. This will be our state:

record Vars =
    array : Array Int,
    i     : Int,

Note. The partition procedure also uses an index j, but we need not include it in the state.

Okay, now let's try and translate partition. I won't do it step-by-step, this is more of a show-off than a tutorial, but I'm sure you'll be able to follow it. Here it is:

func partition : Int -> Int -> Proc Vars Int =
    \lo \hi
    (at hi . array) -> \pivot
    i := lo;
    for (range lo (hi - 1)) (
        \j \next
        (at j . array) -> \at-j
        when (at-j < pivot) (
            \next
            i -> \ii
            array <- swap ii j;
            i <- + 1;
            next
        );
        next
    );
    i -> \ii
    array <- swap ii hi;
    return ii

Details. The swap function has type Int -> Int -> Array a -> Array a and does the obvious: evaluates to an array with the corresponding elements swapped.

It's definitely a little longer than the pseudocode. Most of the extra lines are from the lambdas and getting the current value of i. But otherwise, it reads very similarly.

Now onto the quicksort procedure:

func quicksort : Int -> Int -> Proc Vars Nothing =
    \lo \hi
    if (lo >= hi)
        (return nothing);
    call (partition lo hi) \p
    call (quicksort lo (p - 1));
    call (quicksort (p + 1) hi);
    return nothing

This one is very straightforward. The only thing we changed from the pseudocode is that we inverted the condition. The pseudocode does something when lo < hi, we instead halt the procedure in the other case.

Let's see if this all works.

func main : IO =
    let (
        start-with (Vars (empty 0) 0);
        for-pair (enumerate [2, 6, 1, 0, 4, 3, 5, 9, 7, 8])
            (\i \x (array . at i) := x);
        call (quicksort 0 9);
        return array
    ) \arr
    for (range 0 9) (
        \i \next
        println (string; at i arr);
        next
    );
    quit

In this main function, we first start with an empty array and a zero i variable (which is irrelevant). Then we assign some random numbers to the first 10 indices of the array. Then we quicksort them and bind the resulting array to arr using let. Then we print the first 10 elements and see if it worked:

$ funkycmd quicksort.fn
0
1
2
3
4
5
6
7
8
9

It worked perfectly!

So, as you can see, we can write imperative algorithms quite straightforwardly in Funky!

Forget monad transformers (if you've used Haskell), mixing procedures with IO isn't such a big deal. I'll show you how to do it.

So, we have this code:

func main : IO =
    let (
        start-with (Vars (empty 0) 0);
        for-pair (enumerate [2, 6, 1, 0, 4, 3, 5, 9, 7, 8])
            (\i \x (array . at i) := x);
        call (quicksort 0 9);
        return array
    ) \arr
    for (range 0 9) (
        \i \next
        println (string; at i arr);
        next
    );
    quit

But the let is in fact not needed. Remember, there's an overloaded version of return (which we are in fact using in this code) with this type:

func return : (s -> a) -> Proc s a

How about we used it rather differently than we already have? What if we passed it a function of type Vars -> IO? Something like this:

func main : IO =
    start-with (Vars (empty 0) 0);
    for-pair (enumerate [2, 6, 1, 0, 4, 3, 5, 9, 7, 8])
        (\i \x (array . at i) := x);
    call (quicksort 0 9);
    return \vars                              # <
    for (range 0 9) (                         # <
        \i \next                              # <
        println (string; at i (array vars));  # <
        next                                  # <
    );                                        # <
    quit                                      # <

I marked the function which we passed to return. It took vars, which is the whole state of the above procedure and made some IO out of it. The whole procedure now has type Proc Vars IO and so start-with turns it into just IO. Everything works:

$ funkycmd quicksort.fn
0
1
2
3
4
5
6
7
8
9

That's how we switch from Proc to IO! How do we switch back? Just start-with again! You have the last state, reuse it. We need to make sure, though, that we return some IO at the end.

Here's a simple program that reads 10 numbers from the input and prints out the average after each one (uses the Average record we defined earlier):

func main : IO =
    start-with (Average 0 0);

    for (range 1 10) (
        \i \next
        call average \avg
        return \a
        println ("Current average is " ++ string avg ++ ".");
        print ("Number #" ++ string i ++ ": ");
        scanln; int |> \x
        start-with a;
        call (add x);
        next
    );

    call average \avg
    return \a
    println ("Final average is " ++ string avg ++ ".");
    quit

I'm sure we could shave off some lines in a true imperative language, but so what! It's not bad for a purely functional one.

That's all for this part. In the next part, we'll shine some light on "exception" handling.

What a better way to finish a tour than by talking about failing, right? Different languages solve the problem of failure differently. Many use the concept of exceptions: when an exception occurs, the program breaks its control flow and starts back-tracking the calls until it finds an appropriate exception handler. Other languages, such as Go do it differently, they employ error values that the programmer must manually check.

In this part, we'll talk about how error handling can be done in Funky. Of course, just like pretty much anything else, error handling isn't built-in to the language but is a part of the standard library instead.

The standard library currently only implements the simplest form of error handling: the Maybe type. More sophisticated error types will be added when the need and specific use-cases arise.

Most functions always succeed. But some can also fail. To represent failure, we need a new type. The simplest (and so far only) type for this purpose is Maybe:

union Maybe a = none | some a

It has two alternatives: none and some. The former is a failure. The latter is a success.

Do you remember the list manipulation functions first! and rest!? Well, they crash when the list is empty. Crashing the whole program isn't usually desirable and so there are non-crashing alternatives: first and rest. What do they return? A Maybe of course:

func first : List a -> Maybe a
func rest  : List a -> Maybe (List a)

For example:

func main : IO =
    let [1, 2, 3, 4] \nums
    println (
        switch first nums
        case none
            "nothing there"
        case some \x
            "the first is " ++ string x
    );
    quit

It works:

$ funkycmd maybe.fn
the first is 1

If we don't wanna use the switch, we can use none? and extract! instead:

func main : IO =
    let [1, 2, 3, 4] \nums
    println (
        let (first nums) \maybe-x
        if (none? maybe-x) "nothing there";
        "the first is " ++ string (extract! maybe-x)
    );
    quit

Note. The function extract! can crash, so use at your own risk.

Yet another alternative would be to use ? and map. They're quite simple, but I'll explain them. Here are their types:

func ?   : a -> Maybe a -> a
func map : (a -> b) -> Maybe a -> Maybe b

The ? function takes a default value and a maybe and evaluates to the default value if the maybe is none. Otherwise, it evaluates to the value inside the maybe. For example: 0 ? none evaluates to 0, while 0 ? some 3 evaluates to 3.

The map function transforms the value inside a maybe using the supplied function. If the maybe is none, the result will be none as well. For example: map (+ 1) none results in none, while map (+ 1) (some 3) results in some 4. It works very much like map for lists.

We can use the map function to turn the Maybe Int obtained from first nums into a Maybe String like this:

map (\x "the first is " ++ string x) (first nums)

Then we can use ? to fill the case when the list is empty:

"nothing there" ? map (\x "the first is " ++ string x) (first nums)

And here's the final program:

func main : IO =
    let [1, 2, 3, 4] \nums
    println ("nothing there" ? map (\x "the first is " ++ string x) (first nums));
    quit

That line is quite long. Too long!

But, there's a solution! The functions ? and map have synonyms that are suitable for vertical code. Namely: if-none and let-some.

func if-none  : a -> Maybe a -> a
func let-some : Maybe a -> (a -> b) -> Maybe b

The function if-none is a precise synonym of ?. And the only difference between let-some and map is the order of arguments.

We use let-some to safely extract a value from a maybe:

let-some (first nums) \x
"the first is " ++ string x

The whole thing becomes a new maybe. To turn it into a naked value, we handle the none case:

if-none "nothing there";
let-some (first nums) \x
"the first is " ++ string x

And here's the whole thing:

func main : IO =
    let [1, 2, 3, 4] \nums
    println (
        if-none "nothing there";
        let-some (first nums) \x
        "the first is " ++ string x
    );
    quit

That's more readable!

Note. Of course, there are many cases when ? and map are the right choices. Perhaps this one is too. Depends on your personal preference.

In this short refactoring exercise, we've seen most of the useful Maybe functions: none?, extract!, ?, map, if-none, let-some.

There are some more, like let-::, some?, for-some, filter-some, and when-some. You can try them out on your own.

Just for the sake of giving another example, here's a simple function to get the third element of a list:

func third : List a -> Maybe a =
    \list
    let-some (rest list) \tail
    let-some (rest tail) \tail
    first tail

Or, here's a more complicated example that uses let-:: (used for destructuring lists into the first element and the rest, otherwise very similar to let-some):

func merge : List Int -> List Int -> List Int =
    \left \right
    if-none (left ++ right);
    let-:: left  \l \ls
    let-:: right \r \rs
    if (l < r) (l :: merge ls right);
    r :: merge left rs

func merge-sort : List Int -> List Int =
    \list
    let (length list) \len
    if (len <= 1) list;
    let (take (len / 2) list) \left
    let (drop (len / 2) list) \right
    merge (merge-sort left) (merge-sort right)

Over the course of the last few parts, we've learned how to do for-loops, Python-like generators, and imperative algorithms. What has that got to do with functional programming?

Someone once said: Functional programming makes difficult tasks easy and easy tasks difficult.

What they meant was that while it's often easy to express a complex algorithm in a few (or even one) lines of code, common things, like making a simple interacting command line program can be challenging and not elegant at all.

I believe this is because some problems are just easier to express imperatively. I thus hope that by making imperative idioms easily expressible in Funky, we can have a language where difficult tasks are easy and easy tasks are easy alike. Really difficult tasks will remain difficult, I'm sorry.

So, how does Funky support the proper functional programming idioms? In this part, we'll focus on those, particularly lists: the powerhouse of functional programming, and take a look at some really cool programs.

Our first problem will be to construct the Pascal's triangle as it is called, although it was definitely not first discovered by Blaise Pascal.

It looks like this:

              1
            1   1
          1   2   1
        1   3   3   1
      1   4   6   4   1
    1   5   10  10  5   1
  1   6   15  20  15  6   1
1   7   21  35  35  21  7   1

It's all ones on the edges, but other than that, each number is exactly the sum of the two numbers above it. Those are just the first eight rows, of course, there's infinite number of them. If you're not familiar with the properties of this triangle, I highly recommend checking out the Wikipedia page, they're quite remarkable.

Alright, so let's make Pascal's triangle. Since Funky is lazy, we can express it as an infinite list of rows. Each row of course is a list of integers:

func pascal's-triangle : List (List Int) =
    # ???

Now, the first row is [1]. It would be nice if we make some function that can transform one row into the next one. Then we could use iterate, which works like this:

iterate f x = [x, f x, f (f x), f (f (f x)), ...]

to generate the whole list of rows.

func pascal's-triangle : List (List Int) =
    iterate ??? [1]

What could be the function to transition from one row to the other? The function adjacent comes handy here. It works like this:

adjacent f [x, y, z, w, ...] = [f x y, f y z, f z w, ...]

It pairs each pair of adjacent elements in the list with the supplied function. That's almost exactly what we want. For example:

adjacent (+) [1, 3, 3, 1] => [4, 6, 4]

All that's missing are the ones at the edges. That's easy to fix:

[1] ++ adjacent (+) [1, 3, 3, 1] ++ [1] => [1, 4, 6, 4, 1]

And here's the final function:

func pascal's-triangle : List (List Int) =
    iterate (\row [1] ++ adjacent (+) row ++ [1]) [1]

That's really elegant! Let's move on to another example.

You may have seen this one, but I have included it anyway, because it's so nice. The quick-sort algorithm is a sorting algorithm that works like this:

1. We pick a single element out of the list, we call it a pivot.
2. We divide the list into three groups: less than pivot, more than pivot, equal to pivot.
3. We know the order in which these groups should appear in the final sorted list, so we sort the first two recursively, then put everything together.

Here, we'll use the first element as the pivot for simplicity. The best choice would be the median, which can be found in O(n) time. Choosing the first element may result in O(n^2) time for some lists, especially nearly sorted ones. However, it will be optimal for randomly ordered lists.

The algorithm as described above can be translated to code nearly exactly (we use List Int for simplicity again, but this can be done generally by taking the < function as another argument):

func quick-sort : List Int -> List Int =
    \nums
    if (empty? nums) [];
    let (first! nums)            \pivot
    let (filter (< pivot) nums)  \less
    let (filter (== pivot) nums) \equal
    let (filter (> pivot) nums)  \more
    quick-sort less ++ equal ++ quick-sort more

And that's it! The only little code smell is the use of first!, but that can be easily fixed:

func quick-sort : List Int -> List Int =
    \nums
    if-none [];
    let-some (first nums)        \pivot
    let (filter (< pivot) nums)  \less
    let (filter (== pivot) nums) \equal
    let (filter (> pivot) nums)  \more
    quick-sort less ++ equal ++ quick-sort more

Now it's perfect.

Calculating the derivative of a function is quite easy:

func differentiate : (Float -> Float) -> Float -> Float =
    \f \x
    let 1e-8 \eps
    (f (x + eps) - f (x - eps)) / (2.0 * eps)

Then, we can use it:

differentiate (\x x ^ 2.0)

The above results in a function that's almost equal to:

\x 2.0 * x

As it should be.

So, how about calculating the integral? A function like:

func integrate : (Float -> Float) -> Float -> Float =
    # ???

would be really nice.

We are gonna use the standard method to compute the integral, which is to:

1. Split the interval [0, x] into many equally-sized chunks.
2. Create a rectangle above (under) each of the chunks who's height matches the value of the function at that point.
3. Calculate the area of each of the rectangles.
4. Sum up those areas.

If you don't understand the algorithm, consider watching this video.

We're gonna express the algorithm using the method of threading. Threading means passing an initial value through a series of transformations. It can be expressed very beautifully using the |> operator. As we know, the |> operator works like this:

(x |> f) = (f x)

Now, to pass a value through a series of functions, we would like to write something like this:

x |> f |> g

But, this would get parenthesised as:

x |> (f |> g)

which is not what we want.

However, if you type the expression x |> f |> g in Funky, you find that it actually works! This is because |> has another version that works like the function composition operator:

(f |> g) = (g . f)

When threading, we usually write the code like this, for readability:

x
|> f
|> g

Now, let's get to the integral. First, we're gonna specify the width of each of the rectangles:

func integrate : (Float -> Float) -> Float -> Float =
    \f \x
    let 0.001 \w
    # ...

The width we chose isn't very small, this is for performance reasons: a very small width would result in too many rectangles.

Now we're gonna generate the positions of the individual rectangles:

func integrate : (Float -> Float) -> Float -> Float =
    \f \x
    let 0.001 \w
    iterate (+ w) 0.0
    |> take-while (<= x)
    # ...

We generate an infinite list of w-separated numbers starting from zero, then we cut them at x. Now, we're gonna transform this list into the values of the function at those points:

func integrate : (Float -> Float) -> Float -> Float =
    \f \x
    let 0.001 \w
    iterate (+ w) 0.0
    |> take-while (<= x)
    |> map f
    # ...

Now we're gonna calculate the areas:

func integrate : (Float -> Float) -> Float -> Float =
    \f \x
    let 0.001 \w
    iterate (+ w) 0.0
    |> take-while (<= x)
    |> map f
    |> map (* w)
    # ...

And finally, sum them all up:

func integrate : (Float -> Float) -> Float -> Float =
    \f \x
    let 0.001 \w
    iterate (+ w) 0.0
    |> take-while (<= x)
    |> map f
    |> map (* w)
    |> sum

And that's all! The threading pattern is useful in many situations and usually results in a very readable code, so use it when appropriate.

You have reached the end of the tour. Thank you! I hope you find Funky interesting. It still needs a lot of work, but I'll do my best to make it as good as possible. If you'd like to get on that journey, you're more than welcome to join me on TODO-CHAT-SERVICE, or contribute on GitHub.

And now that you've learned about the language, here are a few articles about stuff that didn't fit in the tour itself.

This is an article that lists most of the idioms frequently used in Funky code. Each idiom is introduced by a name with a link to the place in this tour that describes it, a short description and some schematic code examples.

• Dashes to separate words.

  yield-all right-pad format-table Priority-Queue
  

• Question marks at the end of predicates (functions that return Bool):

  even? odd? whitespace? empty? none? some?
  

• Exclamation marks at the end of partial functions (functions that can crash!):

  first! rest! extract! at!
  

• Special symbols where appropriate:

  + - * / abs^2 let-::
  

Vertical functions

These are the building block of code that reads top to bottom. The example below show some, but not all of the common patterns of types these functions tend to have.

func semicolon-based-1 : V -> V =
    ...

func semicolon-based-2 : A -> V -> V =
    ...

func lambda-based-1 : (B -> V) -> V =
    ...

func lambda-based-2 : C -> (D -> V) -> V =
    ...

func lambda-based-3 : E -> (F -> G -> V) -> V =
    ...

func lambda-based-4 : I -> (J -> V -> V) -> V -> V =
    ...

func usage : V =
    semicolon-based-1;
    semicolon-based-2 a;
    lambda-based-1 \b
    lambda-based-2 c \d
    lambda-based-3 e \f \g
    lambda-based-4 i (
        \j \next
        ...
        next
    );
    ...

If

The if function is used to choose from two alternatives based on a condition.

println (if condition then else);
println (if (x < y) x y);
...

if (n <= 0) 1;
n * factorial (n - 1)

if (invalid? input)
    (println "invalid"; quit);
println "correct!";
...

if (invalid? input) (
    println "your input is wrong!!!";
    println "now you will suffer.";
    ...
);
...

if (op == "+") ...;
if (op == "-") ...;
if (op == "*") ...;
if (op == "/") ...;
if (op == "^") ...;
"invalid operator"

When

The when function is used to conditionally apply/execute a function unlike if which is used to choose between two alternative branches. The imperative analog of when is an if without an else.

when condition function;
...

when (total-price cart < euro 30.0)
    (println "The shipping will not be free.");
...

when (p x) (x ::) (filter xs)

when condition (
    \next
    ...
    next
);
...

Let

Binding values to variables is not a built-in construct in Funky.

let (reverse; range 1 1000000) \numbers
...

let (filter (< pivot) nums)  \left
let (filter (== pivot) nums) \middle
let (filter (> pivot) nums)  \right
...

let-pair (pair "A" 4) \s \x
...

let (
    ...
) \variable
...

Maybe binding

Both of the expressions have type Maybe Int.

let-some (some 7) \x
x + 10

let-some none \x
x + 10

List binding

Both of the expressions have type Maybe something (something is just a placeholder depending on the type of ...).

let-:: [1, 2, 3, 4, 5] \x \xs  # x=1 and xs=[2,3,4,5]
...

let-:: [] \x \xs  # the whole expression is none
...

For

The for function is used to loop over a list of elements. It is functionally equivalent to fold<.

Short for-loop

for list function;
...

for ["A", "B", "C"] println;
quit

for (range 1 10)
    (println . string);
quit

Long for-loop

for list (
    \x \next
    ...
    next
);
...

Looping over pairs

for-pair list-of-pairs (
    \x \y \next
    ...
    next
);
...

for-pair (enumerate names) (
    \i \name \next
    println ("#" ++ string i ++ ": " ++ name);
    next
);
quit

The current idea is that identifiers prefixed with _ will be unexported and importing would work similarly to Go's package system. All files in a single directory would be a part of a single package.

Also, a record with unexported fields wouldn't export its constructor and a union with unexported alternatives would not be switchable by the importer.

No side-effect interpreter is currently fully featured.

Funky aims to be a general purpose language without forgetting about visualizations, GUI, games, and recreational programming. Here are some of the most wanted side-effect interpreters:

• Command line applications with the ability to replace shell scripts.
• GUI built for visualizations and games first, text editors second.
• Web servers.
• Erlang/Go-style concurrent distributed programs.

True power will come with the ability to use multiple side-effect interpreters in a single program. GUI & command line, concurrency & web, or all of them together. Not sure how to do it yet, but it's definitely something that wants to happen.

The switch/case construct is kinda limited at the moment. You need to list all the alternatives in the same order they are defined.

This construct will be improved to support:

• Listing alternatives in any order.
• A default case + ability to leave out alternatives.
• Switching on multiple things simultaneously.
• Switching on plain values using ==.

Currently, it's possible to make a sum function of this type:

func sum : List Int -> Int

Or this type:

func sum : List Float -> Float

And also other types that can be summed.

While the implementations will look very similar (or even the same), there's no way to generalize them. Just List a -> a won't work, because there's no way to add arbitrary types.

This is where the with clause comes handy:

with zero : a
with +    : a -> a -> a
func sum  : List a -> a = fold> (+) zero

This says that the sum function works on all types a, such that there are functions zero and + with the specified types.

The syntax is currently planned as shown - you need to use multiple with clauses to require multiple functions.

Another example would be:

with string : a -> String
func string : List a -> String =
    \list
    "[" ++ join ", " (map string list) ++ "]"

With regards to type collisions, the type of the sum function is List a -> a. If you attempted to also define a more specific version, like sum : List Int -> Int, it would fail with a type collision. This is a deliberate design choice to avoid having to select "the most specific" version and confuse everybody and instead have it simple: either it's general, or it's specific.

This feature would make a function be applied automatically when needed. This would usually be useful for automatic type-conversions.

An example:

implicit a -> Maybe a = some

The definition looks just like a definition of a normal function, except it starts with implicit instead of func and has no name.

This implicit function would enable writing this:

[1, 2, none, 4, 5, none, none]

instead of this:

[some 1, some 2, none, some 4, some 5, none, none]

The current idea is that an implicit function would only be applied when the original expression doesn't fit the context and only one implicit function could be applied to a single expression.

Also, defining an implicit function:

implicit A -> B = ...

would make types A and B collide.

So, for example, with the above a -> Maybe a conversion, these functions would collide even though they didn't before:

func int : String -> Int
func int : String -> Maybe Int

This is to avoid confusion and ambiguity.

This feature has a potential for abuse, that's why it's only considered and not planned yet.

Instead of the previous feature (implicit functions), I am now considering a more specific approach and that is to lift values and functions so that they are automatically usable for values of container types supporting certain (monadic) operations.

The goal is to be able to do stuff like this:

# Maybe is a monadic container
let (some 3)  \mx
let (some 5)  \my
mx + my  # => some 8

# Functions are monadic containers, too
record Person = name : String, age : Int

func adults : List Person -> List Person =
    filter (age >= 18)  # => (age >= 18) gets automatically transformed to (\p age p > 18)

As you can see, we would be able to use containers like Maybe a as regular unboxed values and apply operations to them, getting containerized values back (some 9 + none would result in none).

To implement this feature, a programmer would need to specify two functions for a monadic container type M a. Those two functions would have to have these types:

a -> M a
M a -> (a -> M b) -> M b

For example:

some     : a -> Maybe a
let-some : Maybe a -> (a -> Maybe b) -> Maybe b

Or:

return : a -> Proc s a
call   : Proc s a -> (a -> Proc s b) -> Proc s b

The programmer would specify these two functions using a new autolift syntax:

autolift some, let-some
union Maybe a = none | some a

autolift return, call
union Proc s a = return a | view (s -> Proc s a) | update (s -> s) (Proc s a)

The type-checker would then insert these two functions whenever necessary to lift plain values and functions.

A few things still need to be figured out, namely the specific algorithm to insert the lifting functions, and implications for type collisions.

The Box type (could also be named Any) would be a built-in type with two built-in functions:

func pack    : a -> Box
func unpack! : Box -> a

The unpack! function could possibly have type Box -> Maybe a and be called unpack.

It would make it possible to temporarily escape the type system and allow creating some type-safe constructs not possible without it.

For example, suppose we'd like to make a side-effect interpreter for Erlang/Go-style concurrency. A natural way would be to define a Routine type, something like this:

union Routine a =
    halt                           |
    make (Chan a -> Routine a)     |
    send (Chan a) a (Routine a)    |
    recv (Chan a) (a -> Routine a) |
    spawn (Routine a) (Routine a)  |

This would enable expressing routines that make channels and send and receive values on them. The interpreter would handle actually sending values over the channels.

There's one crucial deficiency: all channels have to be of the same type. The current type system doesn't make it possible to express it any other way. You can try! It can't be done.

Obviously, we'd like to make channels of different types. Here's how the Box type would help:

union Routine =
    halt                       |
    _make (Box -> Routine)     |
    _send Box Box Routine      |
    _recv Box (Box -> Routine) |
    spawn Routine Routine      |

Three commands are prefixed with _. This means that they're not meant to be used by the user of this library and the future package system will make sure they're unexported.

The Routine type has also lost its type variable. It doesn't need it anymore.

Now, this definition allows sending arbitrary values over arbitrary channels but doesn't guarantee type-safety. However, if we define our own versions of those three commands, we get the type safety back:

record Chan a = _box : Box

func make : (Chan a -> Routine) -> Routine =
    \fnext
    _make \box-ch
    fnext (Chan box-ch)

func send : Chan a -> a -> Routine -> Routine =
    \ch \x \next
    _send (_box ch) (pack x);
    next

func recv : Chan a -> (a -> Routine) -> Routine =
    \ch \fnext
    _recv (_box ch) \box-x
    fnext (unpack! box-x)

These functions guarantee type-safe sending and receiving over channels and make it possible to create channels of different types.

Currently, we can only partially apply the first argument of a prefix function without making a lambda:

map sqrt

To partially apply a second argument, we need to make a lambda:

\f map f [1, 2, 3, 4, 5]

This syntax would make it possible to partially apply the second, third, or any other argument without making a lambda:

map _ [1, 2, 3, 4, 5]

Funky current allows type annotations like this:

expression : type

And also like this:

some-function \(variable : type)
rest-of-the-code

But this notation can be very cumbersome in many cases.

TODO: examples

The idea therefore is to add an option to accept an explicit type parameter. This can only be a parameter. The syntax would look like this:

func unpack : type a -> Box -> Maybe a